新しい情報代数学の構築
～曖昧さを許容する数理体系を
　目指して～

● 研究テーマ

• ❖ ファジィ数理論を用いた情報代数学の研究
• ❖ 曖昧さを許容する回帰分析や因子分析の構築
• ❖ ファジィ理論の人の知覚認識への応用

● キーワード

ファジィ理論・情報代数学

● 実施中の研究概要

ファジィ理論は、曖昧さを許容し得ることを特徴とする数学です。厳密にただ一つの値をとる通常のクリスプな数に対して、やや幅をもった値をとるファジィ数を基にして、論理・集合・写像・関係といった数学的対象をとらえ、その上に代数学や解析学を構築しようとするものです。ファジィ理論で用いられる数理は、曖昧さを含む人の知覚を表すのに適していると考えられます。言葉のもつ音韻・音楽から受ける印象・色や形から受ける印象など、人の受ける感覚的な印象を科学的に捉え、それを計算機で扱うことができれば、計算機の利用環境を大いに向上できると考えられます。
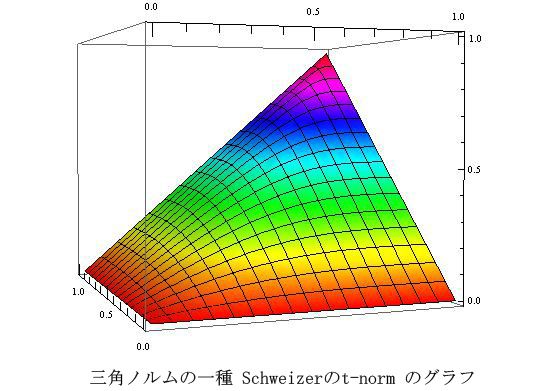
私はこのような方向性の中で、ファジィ理論で用いられる数理や演算に関する研究と、それを利用した人の認識や意思決定の理論に関する研究を行ってきました。ファジィ理論においては、三角ノルムと呼ばれる演算が用いられ、これは数理演算としては乗算、論理演算としては連言に相当する極めて基本的かつ重要な演算となっています。その性質を見極め、個々の問題解決に適した三角ノルムを構成することは、ファジィ理論の応用技術として極めて重要であると考えられます。これまで取り組んできたファジィ数理モデルの構成に関する知見に基づいて、人の主観に関わる様々な分析に有効に働くような、ファジィ数理的代数系の構築といったテーマに取り組んでみたいと考えます。人の持つ主観的な印象を科学的に捉えるというテーマは、難しい研究テーマではありますが、人にとってより快適な計算機環境を構築する上で、大切な基礎的技術になると考え、このテーマに取り組んでいます。

● 過去の論文や著書などの業績

【論文】t-ノルムおよびt-コノルムから導出される行列演算とその応用
　（日本知能情報ファジィ学会誌「知能と情報」、第22巻,、第4号 pp. 472-480（2010年））

● 関連リンク先

❖ より詳しい研究者データ

• https://hyokadb02.jimu.kyutech.ac.jp/html/194_ja.html